La integración de todos los datos requiere la transformación entre todos los Sistemas de Referencia que entran en juego.
El ciclo que se expone a continuación podría ser en otro orden, pero entendemos que es la forma más racional de tratarlo:
Coordenadas en el Sistema Geodésico
En el sistema Astronómico Medio se conocen del punto (Φ, L, H) y el acimut de una dirección A; para pasar a un sistema geodésico se ha de hacer a través del conocimiento de las componentes de la desviación de la vertical (ς, n), y la ondulación del geoide respecto al elipsoide de referencia. Así, las coordenadas geodésicas del punto serán:
Y el acimut geodésico 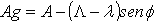
Coordenadas en el Sistema Cartesiano Global
En el Sistema Geodésico se conocen (φ, λ, h) para pasar al Sistema Cartesiano Global centrado en el elipsoide de parámetros (a, e2 ) será:
Coordenadas en el Sistema Astronómico Local
Para obtener en topografía incrementos de
coordenadas entre dos puntos a partir de la observación con GPS, donde se conoce realmente (ΔX, ΔY, ΔZ) para calcularlos en un Sistema Astronómico Local o bien Geodésico Local, será:
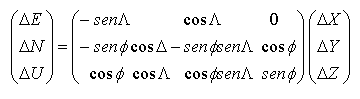
Si utilizásemos φ,λ, sería Geodésico Local.
Datos para Replanteo
Si en el ámbito de la topografía se tuviese que replantear habría que calcular el acimut, distancia y ángulo cenital, así:
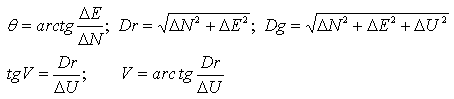
Proceso Inverso
El proceso inverso seguiría el mismo orden:
. Se mide Dg, Θ, V.
. Se calcula Dr = Dg ·senV ; DE=Dr ·senΘ ; DN=Dr ·cosΘ ; DU=Dg ·cosV
Se calcula:
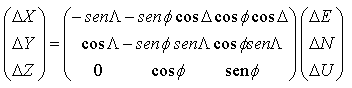
Se calcula:
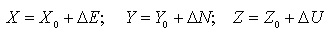
Se calcula:
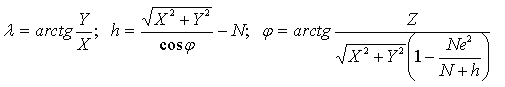
Se calcula:
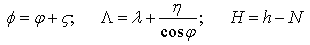
|